作为《工程经济》最难的公式集中地带,年金A、现值P、终值F的计算题确实很让人头疼。但其实细细品来无非就是6个公式,不过在学习这几个公式之前,一定要先掌握复利的公式,一切源于复利,终于延伸。
复利计算公式:假设本金为P,年利率为i,存款年限为n,那么复利计算公式为:F=P×(1+i)ⁿ。
年金A,发生在期末、连续、等额,且最后一个年金与终值F发生在一个时点。
现值P,这个P的时间节点在期初,也可以理解为还没又开始计息。
P:现值,发生在0时点,即第1期期初
F:终值,发生在n时点,即第n期期末
A:等额年金发生在1→n时点,表示1→n每期的期末。
(这里要注意一下,P在期初,A在期末,所以比A早整整1年,而A与F则重合于n点)
例题1:某投资人5年内每年末投资100万元,年收益率4.8%,按复利计算问第5年末总收益(含投资本金)为多少? 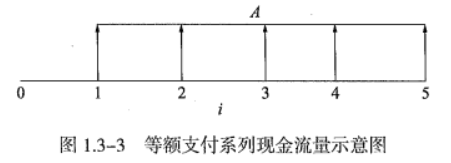
先用复利的方法计算一下。1年100万、2年100万、3年100万、4年100万这几个是需要复利的,但是第5年这个属于存进去立刻获得0收益,这个不要忘,那么计算式就变成了:
①100×(1+4.8%)⁴=120.6272(第一年末的总共复利4次,因为是年末投入)
②100×(1+4.8%)³=115.1023
③100×(1+4.8%)²=109.8304
④100×(1+4.8%)¹=104.8
⑤100
120.6272+115.1023+109.8304+104.8+100=550.3599万元
如果用公式诚然会更加简单,公式![]()
F=100×[(1+4.8%)⁵-1]÷4.8%=550.3598
例题2:某企业从现在起连续5年每年年初向银行贷款1000万元,年利率12%,半年复利计息一次,第5年年末一次还清本利和( )万元。
A.6353 B.6399 C.7189 D.13181
这道题比上一道题诚然难上不少,5年连续年初借款1000万元,然后求第5年年末本利和。这个直接用公式肯定不行,因为年金A应该发生在年末,我们先要把年金A折算到期末,设为A⁺。因为半年复利一次,金A⁺=1000(1+12%÷2)²=1123.6万元,年有效利率i=(1+12%÷2)²-1=12.36%
根据公式![]() 计算,F=1123.6×[(1+12.36%)⁵-1]÷12.36%=7189.2918万元
计算,F=1123.6×[(1+12.36%)⁵-1]÷12.36%=7189.2918万元
如果用复利方法计算:
①1000×(1+12%÷2)¹⁰=1790.8477
②1000×(1+12%÷2)⁸=1593.8480
③1000×(1+12%÷2)⁶=1418.5191
④1000×(1+12%÷2)⁴=1262.7470
⑤1000×(1+12%÷2)²=1123.6
合计后等于7189.0978
两种计算结果虽然有误差,但不影响C这个正确答案。
例题3:某企业5年内每年年初从银行提款10000元,银行存款年利率为10%,按年复利计息,则期初应存入银行的资金是( )元。
A.37910 B.41699 C.4355 D.50000
这题是已知年金求现值,如果用上述第二种类型不记忆公式,则往回折现,以第5年年初的10000元计算,这个10000共计经过计息4次,第5年年初即第4年年末,P=10000÷(1+10%)⁴=6830.1345元,依次计算1、2、3、4很容易得出结果B。
如果采用公式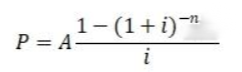 ,这个公式同样不能直接使用,需要先将10000元折算到年末,计算出年金A,A=10000×(1+10%)=11000元。
,这个公式同样不能直接使用,需要先将10000元折算到年末,计算出年金A,A=10000×(1+10%)=11000元。
P=11000[1-(1+10%)⁻⁵]÷10%=41698.6545
以上三道例题的两种做题方法看似都可以,也各有优缺点,第二种不用记忆公式,但计算起来会有些繁琐。公式主要有六个:
FA=发 已知年金求终值: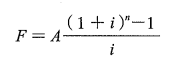 ,已知终值求年金
,已知终值求年金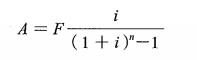 (年金A,期末、连续、等额,最后一个A与终止F为同时点)
(年金A,期末、连续、等额,最后一个A与终止F为同时点)
PA=怕 已知现值求年金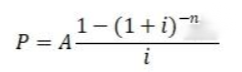 ,已知年金求现值
,已知年金求现值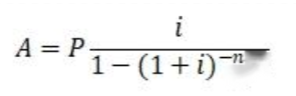 (买房按揭型) (P与年金A间隔一期,A处于期末)
(买房按揭型) (P与年金A间隔一期,A处于期末)
已知现值求终值即复利公式F=P(1+i)ⁿ,已知终值求现值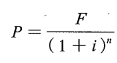
这里备注一下,现值、年金的公式和《工程经济》课本上给的是不一致的,课本上的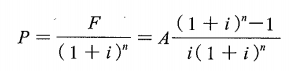 说实话不是很好记忆。
说实话不是很好记忆。
两种写法
1、![]() :i、n固定知道P,求F
:i、n固定知道P,求F
2、![]() :i、n固定知道F,求P
:i、n固定知道F,求P
重点重复
形式和特征:P比A早一期,A与F重合于n点
比较大小
在P一定,n相同时,i越高,F越大;在i相同时,n越长,F越大;
在F一定,n相同时,i越高,P越小;在i相同时,n越长,P越小。
i、n相同时,F与P呈同向变化。F越大,P越大;F越小,P越小
重点题型
若10年内,每年年初存入2000元,i=6%,10年后本息和多少?(27943.29)

知识类文章,仅用于个人学习、研究、欣赏,如涉及侵权或拒绝展示,请及时联系邮箱1295@163.com删除。
转载请注明:秀日 » 一文教你快速掌握经济中年金A、现值P、终值F的计算方法